Kohlrausch’s law states that at infinite dilution, each ion contributes a fixed amount to the molar conductivity, independent of other ions. The total conductivity of an electrolyte is the sum of the contributions of its cations and anions. It is used to determine limiting molar conductivity, ion mobilities, and dissociation constants.
At infinite dilution, the equivalent conductance of an electrolyte is equal to the sum of the equivalent conductances of its individual ions.
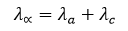
Here, the equivalent conductance of the anion and the cation are denoted separately.
For example, at 25°C, the equivalent conductance of NaCl at infinite dilution is found to be 126.45 ohm⁻¹ cm² eq⁻¹.
The equivalent conductance of the Na⁺ ion is 50.11 ohm⁻¹ cm² eq⁻¹, and that of the Cl⁻ ion is 76.34 ohm⁻¹ cm² eq⁻¹.
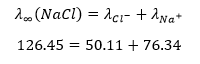
Watch full lecture in Hindi/Urdu
Watch full lecture in English
Applications
(1) Calculation of λ∞ for Weak electrolytes
Weak electrolytes do not ionize significantly in solution and remain largely unionized even at very high dilution. As a result, it is not practically possible to determine their equivalent conductance at infinite dilution (Λ∞) through direct measurement. However, Λ∞ can be calculated indirectly using Kohlrausch’s Law of Independent Migration of Ions.
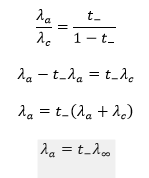
The ionic conductance of an ion can be determined by multiplying the equivalent conductance at infinite dilution of a strong electrolyte containing that ion by its transport number.
Using this method, the ionic mobilities of both ions in a weak electrolyte can be calculated.
By adding the conductances of the individual ions, the equivalent conductance at infinite dilution (Λ∞) of the weak electrolyte can then be obtained.
(2) Calculation of Absolute Ionic mobilities
The absolute ionic mobility of an ion is defined as the velocity of an ion in centimetres per
second under a potential gradient of one volt per centimetre. (Potential gradient = applied EMF/
distance between (the electrodes). It is expressed in cm sec–1.
For example, if the velocity of an ion at infinite dilution is cm/s, and the distance between the electrodes is 20 cm with an applied voltage of 100 V, the potential gradient is 100/20 i.e., 5 volts per cm. Therefore, the ionic mobility is U/5 cm sec–1.
(3) Calculation of the solubility of sparingly soluble salts
Substances such as AgCl or PbSO₄, commonly referred to as insoluble, actually have a definite solubility in water. This solubility can be determined by measuring the conductance of their saturated solutions. Because only a very small amount of solute is present, it is assumed to be completely dissociated into ions even in a saturated solution. Therefore, the equivalent conductance (κV) equals the equivalent conductance at infinite dilution. According to Kohlrausch’s Law, this is the sum of the ionic mobilities
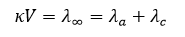
By knowing the values of κ (specific conductance) and (equivalent conductance at infinite dilution), the volume
— in milliliters — containing one gram-equivalent of the electrolyte can be calculated.
Download Complete Notes Below
(4) Calculation of the Degree of Dissociation or Conductance Ratio
The apparent degree of dissociation, of an electrolyte at the dilute
is given by
where
is the equivalent conductance of the electrolyte at the dilution
and
is its equivalent conductance at infinite dilution. This according to Kahlrausch’s Law is the sum of
and
.
(5) Calculation of the Ionic product for water
The observed specific conductance of the purest water at is
The conductance of one litre of water containing 1 gram eqvt of it would be:
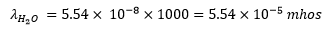
At the same temperature the conductance of ions and
ions are :
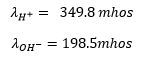
According to Kohlrausch’s Law
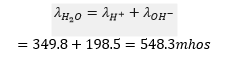
One molecule of water gives one ion and
ion
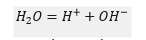
Assuming that ionic concentration is proportional to conductance, we have
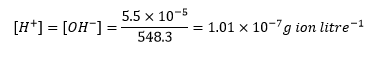
The ionic product of water is then
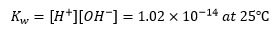
For most purposes, the value of is taken to be
I’m very happy to read this. This is the type of manual that needs to be given and not the…
Proudly Powered By




Leave a Comment